dew's CSE Studying
05 큐(C언어로 쉽게 풀어쓴 자료구조) 본문
5.1 큐 추상 데이터 타입
큐(queue): 먼저 들어온 애가 먼저 나가는 선입선출(FIFO:First In First Out)구조의 자료구조
마트에서 줄 서는 거를 생각하자!!
계속 쌓이는 스택의 경우 데이터의 추가와 삭제가 같은 쪽에서 일어났지만 큐는 전단(front)에서 삭제가, 후단(rear)에서 삽입이 일어난다!
큐의 ADT:
-객체: 0개 이상의 요소들로 구성된 선형 리스트
-연산:
create(max_size) ::= 최대 크기가 max_size인 공백큐를 생성
init(q) ::= 큐를 초기화
is_empty(q) ::=
if(size==0) return TRUE;
else return FALSE;
is_full(q) ::=
if(size==max_size) return TRUE;
else return FALSE;
enqueue(q,e) ::=
if(is_full(q)) queue_full 오류;
else q의 끝에 e를 추가한다
dequeue(q) ::=
if(is_empty(q)) queue_empty 오류;
else q의 맨 앞에 있는 e를 제거하여 반환한다
peek(q) :=
if(is_empty(q)) queue_empty 오류;
else q의 맨 앞에 있는 e를 읽어서 반환한다5.2 선형큐
1차원 배열을 이용하여 선형큐를 만들어보자
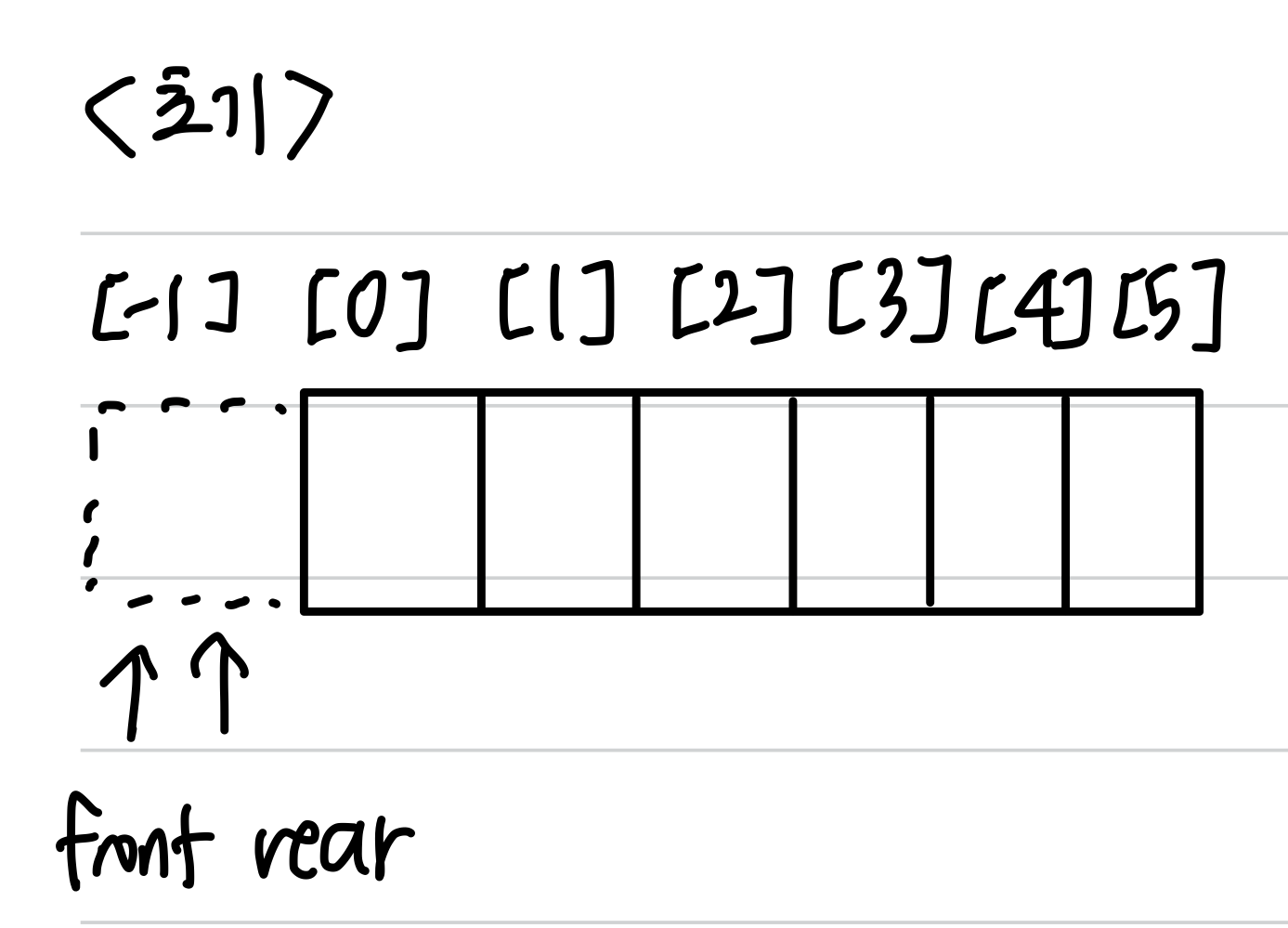
크기가 5인 1차원 배열 형태의 큐를 만들어보았다. 초기상태에는 front와 rear가 둘다 -1을 가리키고 있다
데이터 삽입: rear를 +1 -> 그 자리에 데이터 삽입
데이터 삭제: front +1 -> 그 자리의 데이터를 삭제
선형큐의 구현
#include <stdio.h>
#include <stdlib.h>
#define MAX_QUEUE_SIZE 5
typedef int element;
typedef struct {
int front;
int rear;
element data[MAX_QUEUE_SIZE];
} QueueType;
//오류함수
void error(char *message)
{
fprintf(stderr, "%s\n", message);
exit(1);
}
//init_queue(초기화)
void init_queue(QueueType *q)
{
q->rear=-1;
q->front=-1;
}
//queue_print(출력)
void queue_print(QueueType *q)
{
for(int i=0; i<MAX_QUEUE_SIZE; i++){
if(i<=q->front || i>q->rear)
printf(" | " );
else
printf("%d | ", q->data[i]);
}
printf("front=%d, rear=%d", q->front, q->rear);
printf("\n");
}
//is_full
int is_full(QueueType *q)
{
if(q->rear == MAX_QUEUE_SIZE-1) //rear가 마지막 인덱스를 가리키고 있으면
return 1;
else
return 0;
}
//is_empty
int is_empty(QueueType *q)
{
if(q->front == q->rear) //front와 rear이 같은 인덱스를 가리키면
return 1;
else
return 0;
}
//enque(q, item)
void enqueue(QueueType *q, int item)
{
if (is_full(q)) {
error("큐가 포화상태입니다.");
return;
}
q->data[++(q->rear)] = item;
}
//dequeue(q, item)
//반환값이 있는 애들은 void가 아니라 int로 정의~
int dequeue(QueueType *q)
{
if (is_empty(q)) {
error("큐가 공백상태입니다.");
return -1;
}
int item = q->data[++(q->front)];
return item;
}
//main함수
int main(void)
{
int item=0;
QueueType q;
init_queue(&q);
enqueue(&q, 10); queue_print(&q);
enqueue(&q, 20); queue_print(&q);
enqueue(&q, 30); queue_print(&q);
item = dequeue(&q); queue_print(&q);
item = dequeue(&q); queue_print(&q);
item = dequeue(&q); queue_print(&q);
return 0;
}
공부를 위해 front와 rear의 위치도 함께 출력하도록 해보았다 :) 공백큐가 되면 front==rear이 되는 것을 확인할 수 있다.
**선형큐의 단점: front와 rear의 값이 계속 증가만 하기 때문에 언젠가는 배열의 끝에 도달하게 되고, 배열의 앞부분이 비어있더라도 사용하지 못한다
얘를 해결하기 위해 주기적으로 위치를 왼쪽으로 shift해줄 수 있지만 상당히 시간이 걸리고 코딩이 복잡해진다.
얘를 해결하기 위한 방법이 바로 선이 아닌 원을 사용하는 원형큐이다!!!!
5.3 원형큐

얘는 선형큐와 차이가 있다. 일단 선형큐에서는 초기상태가 front == rear == -1였는데 여기서는 front와 rear가 -1이 아닌 0을 가리키며 시작한다.
데이터 삽입: rear를 +1 -> 그 자리에 데이터 삽입
데이터 삭제: front +1 -> 그 자리의 데이터를 삭제
요 데이터 삽입/삭제의 원리는 동일하다
원형큐에서도 선형큐와 마찬가지로 front==rear일때 큐가 비어있음을 의미한다.

공백큐 상태에서 A~G까지 7개의 요소를 삽입했다고 가정해보자. 이걸 우린 포화상태라고 한다. 원형큐에서는 포화상태와 공백상태를 구분하기 위해 항상 하나의 자리를 비워놓기 때문이다.
공백큐에서,
front == rear -> 공백상태
front = rear-1 -> 포화상태
만약 요소들의 개수를 저장하고 있는 추가 변수 count가 존재한다면 한 자리를 비워두지 않아도 된다.
원형큐의 삽입, 삭제 알고리즘
front <- (front+1)%MAX_QUEUE_SIZE
rear <- (rear+1)%MAZ_QUEUE_SIZE
우리는 나머지 연산자를 사용하여 front와 rear의 인덱스 위치를 정해줄 것이다. 이건 인덱스가 마냥 증가하면 안되고 원이니까 반복되야 하기 때문이다. 만약 최대 인덱스인 MAX_QUEUE_SIZE -1 에서 하나가 증가하면 나머지가 0이 되어 다시 인덱스가 0이 된다
원형큐의 구현
#include <stdio.h>
#include <stdlib.h>
// ====원형큐 코드 시작====
#define MAX_QUEUE_SIZE 5
typedef int element;
typedef struct {
element data[MAX_QUEUE_SIZE];
int front, rear;
} QueueType;
//오류함수
void error(char *message)
{
fprintf(stderr, "%s\n", message);
exit(1);
}
//init_queue(초기화)
void init_queue(QueueType *q)
{
q->front = q->rear = 0;
}
//is_full
//front = rear+1 이면 포화
int is_full(QueueType *q)
{
return((q->rear +1)%MAX_QUEUE_SIZE == q->front);
}
//is_empty
//front==rear 이면 공백
int is_empty(QueueType *q)
{
return (q->front == q->rear);
}
//queue_print(출력)
void queue_print(QueueType *q)
{
printf("QUEUE(front=%d rear=%d) = ", q->front, q->rear);
if (!is_empty(q)) {
int i = q->front;
do {
i = (i+1) % (MAX_QUEUE_SIZE);
printf("%d | ", q->data[i]);
if (i==q->rear) //front==rear이면 empty
break;
} while (i != q->front);
}
}
//enque(q, item)
void enqueue(QueueType *q, int item)
{
if (is_full(q))
error("큐가 포화상태입니다.");
q->rear = (q->rear +1)%MAX_QUEUE_SIZE; //rear을 +1해주고
q->data[++(q->rear)] = item; //반환
}
//dequeue(q, item)
element dequeue(QueueType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다.");
q->front = (q->front +1)%MAX_QUEUE_SIZE;
return q->data[q->front];
}
//peek
element peek(QueueType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다.");
return q->data[(q->front+1)%MAX_QUEUE_SIZE];
}
//main함수
int main(void)
{
QueueType queue;
int element;
init_queue(&queue);
printf("--데이터 추가 단계--\n");
while (!is_full(&queue)) {
printf("정수를 입력하시오: ");
scanf("%d", &element);
enqueue(&queue, element);
queue_print(&queue);
}
printf("큐는 포화상태입니다.\n\n");
printf("--데이터 삭제 단계--\n");
while (!is_empty(&queue)) {
element = dequeue(&queue);
printf("꺼내진 정수: %d \n", element);
queue_print(&queue);
}
printf("큐는 포화상태입니다.\n\n");
return 0;
}
5.4 큐의 응용: 버퍼
큐의 실제 사용: 서로 다른 속도로 실행되는 두 프로세스 간의 상호작용을 조화시키는 버퍼역할
5.5 덱이란?
덱(deque, double-ended queue):큐의 front와 rear에서 모두 삽입/삭제가 가능한 큐(여전히 중간 삽입/삭제는 불가능!)

덱은 스택과 큐의 연산을 모두 가지고 있다. 덱의 전단에서만 삽입/삭제를 하면 스택이 되고, 후단에 삽입/전단에 삭제를 한다면 큐가 된다. 이처럼 스택,큐에 비해 융통성이 있는 자료구조임을 알 수 있다.
배열을 이용한 덱의 구현
#include <stdio.h>
#include <stdlib.h>
#define MAX_QUEUE_SIZE 5
typedef int element;
typedef struct {
element data[MAX_QUEUE_SIZE];
int front, rear;
} DequeType;
//add_front
void add_front(DequeType *q, element val){
if (is_full(q))
error("큐가 포화상태입니다");
q->data[q->front] = val;
q->front = (q->front -1 + MAX_QUEUE_SIZE)%MAX_QUEUE_SIZE;
}
//delete_rear(뒷단을 삭제)
element delete_rear(DequeType *q){
int prev = q->rear;
if (is_empty(q))
error("큐가 공백상태입니다");
q->rear = (q->rear -1 + MAX_QUEUE_SIZE)%MAX_QUEUE_SIZE;
return q->data[prev];
}
//get_rear(뒷단을 반환)
element get_rear(DequeType *q){
if (is_empty(q))
error("큐가 공백상태입니다");
return q->data[q->rear];
}새로 추가된 부분들만 코드로 작성해보았다
5.6 큐의 응용: 시뮬레이션
'3-1 > 자료구조 again' 카테고리의 다른 글
| 09 우선순위 큐 (C언어로 쉽게 풀어쓴 자료구조) (2) | 2024.10.23 |
|---|---|
| 08 트리 (C언어로 쉽게 풀어쓴 자료구조) (3) | 2024.10.23 |
| 07 연결리스트2 (C언어로 쉽게 풀어쓴 자료구조) (5) | 2024.10.19 |
| 06 연결리스트1 (C언어로 쉽게 풀어쓴 자료구조) (8) | 2024.10.18 |
| 2.4 하노이탑 문제 출력값을 분석해보자! (1) | 2024.10.14 |




